Benchmark Dose (BMD) Methods
This Methodology page has been excerpted from the U.S. Environmental Protection Agency (USEPA) Benchmark Dose Technical Guidance document, published in 2012. The Technical Guidance goes into more depth on each issue, including examples illustrating the process and equations for selected benchmark dose (BMD![]() BMDAn exposure due to a dose of a substance associated with a specified low incidence of risk, generally in the range of 1% to 10%, of a health effect; or the dose associated with a specified measure or change of a biological effect.) models.
BMDAn exposure due to a dose of a substance associated with a specified low incidence of risk, generally in the range of 1% to 10%, of a health effect; or the dose associated with a specified measure or change of a biological effect.) models.
This Methodology page provides a high-level introduction to the computing BMDs, their lower confidence limits (BMDLs), data requirements, dose-response analysis, and USEPA reporting requirements that are specific to the use of BMDs and BMDLs. Pointers are provided to relevant web pages or documents that describe the functions and capabilities of the Agency's Benchmark Dose Software (BMDS), which was designed to facilitate applying the BMD methods described in the Technical Guidance.
On this page, BMD is used generically to refer to the benchmark dose approach; in the specific cases of characterizing model results, BMD and BMC![]() BMCThe concentration of a substance inhaled that is associated with a specified low incidence of risk, generally in the range of 1% to 10%, of a health effect; or the concentration associated with a specified measure or change of a biological effect.
BMCThe concentration of a substance inhaled that is associated with a specified low incidence of risk, generally in the range of 1% to 10%, of a health effect; or the concentration associated with a specified measure or change of a biological effect.![]() BMC
BMC![]() BMCThe concentration of a substance inhaled that is associated with a specified low incidence of risk, generally in the range of 1% to 10%, of a health effect; or the concentration associated with a specified measure or change of a biological effect.The concentration of a substance inhaled that is associated with a specified low incidence of risk, generally in the range of 1% to 10%, of a health effect; or the concentration associated with a specified measure or change of a biological effect. refer to central estimates. BMDL
BMCThe concentration of a substance inhaled that is associated with a specified low incidence of risk, generally in the range of 1% to 10%, of a health effect; or the concentration associated with a specified measure or change of a biological effect.The concentration of a substance inhaled that is associated with a specified low incidence of risk, generally in the range of 1% to 10%, of a health effect; or the concentration associated with a specified measure or change of a biological effect. refer to central estimates. BMDL![]() BMDLA lower one-sided confidence limit on the BMD. or BMCL
BMDLA lower one-sided confidence limit on the BMD. or BMCL![]() BMCLA lower one-sided confidence limit on the BMC. refer to the corresponding lower limit of a one-sided 95% confidence interval on the BMD or BMC, respectively. This is consistent with the terminology introduced by Crump (1995) and with that used in BMDS.
BMCLA lower one-sided confidence limit on the BMC. refer to the corresponding lower limit of a one-sided 95% confidence interval on the BMD or BMC, respectively. This is consistent with the terminology introduced by Crump (1995) and with that used in BMDS.
Note: Because applying the BMD approach and interpreting the results can be technically challenging, it is recommended that BMD modeling be performed by or in collaboration with personnel expert in the statistical procedures and potential pitfalls of this type of analysis. The Technical Guidance document discusses in more detail a number of issues that support consistent application of the BMD approach.
- Introduction
- Before Starting a BMD Analysis
- Decision Tree for BMD Modeling
- Selecting the Benchmark Response Level (BMR)
- Modeling the Data
- Assessing How Well the Model Describes the Data
- Global Goodness of Fit Measures (p values)
- Scaled Residuals at Each Dose Level
- Graphical Displays
- Improving Model Fit
- Comparing Models
- Within a Family of Models: the Akaike Information Criterion (AIC)
- Other Considerations
- Calculating Confidence Limits to Get a BMDL
- Selecting the Model to Use for POD Computation
- Reporting Recommendations
Introduction
The USEPA conducts human health risk assessments for an array of health effects that may result from exposure to environmental agents. These assessments often include an analysis of the dose-response relationship between exposure and health-related outcomes.
- Defining a point of departure (POD
 PODThe point on a dose-response curve established from experimental data, e.g., the benchmark dose, generally corresponding to an estimated low effect level (e.g., 1% to 10% incidence of an effect). Depending on the mode of action and available data, some form of extrapolation below the POD may be employed for low-dose risk assessment or the POD may be divided by a series of uncertainty factors to arrive at a reference dose.)
PODThe point on a dose-response curve established from experimental data, e.g., the benchmark dose, generally corresponding to an estimated low effect level (e.g., 1% to 10% incidence of an effect). Depending on the mode of action and available data, some form of extrapolation below the POD may be employed for low-dose risk assessment or the POD may be divided by a series of uncertainty factors to arrive at a reference dose.) - Extrapolating from the POD to a human exposure level that is not expected to cause an appreciable health risk (e.g., a Reference Dose
 Reference DoseAn estimate (with uncertainty spanning perhaps an order of magnitude) of a daily oral exposure to the human population (including sensitive subgroups) that is likely to be without appreciable risk of deleterious effects during a lifetime.) or to an estimate of the potency (risk/dose) of the chemical (e.g., Cancer Potency
Reference DoseAn estimate (with uncertainty spanning perhaps an order of magnitude) of a daily oral exposure to the human population (including sensitive subgroups) that is likely to be without appreciable risk of deleterious effects during a lifetime.) or to an estimate of the potency (risk/dose) of the chemical (e.g., Cancer Potency Cancer PotencyA number that estimates the cancer risk (incidence) for a lifetime exposure to a substance per unit of dose. Dose is generally expressed as mg/kg body wt/day., also called the Cancer Slope Factor)
Cancer PotencyA number that estimates the cancer risk (incidence) for a lifetime exposure to a substance per unit of dose. Dose is generally expressed as mg/kg body wt/day., also called the Cancer Slope Factor)
The purpose of the Benchmark Dose Technical Guidance and these training materials is to provide guidance on how to consistently apply the BMD approach in order to derive BMDs and BMDLs. The BMD approach is principally used by the USEPA for determining PODs for the derivation of Reference Values (USEPA, 2002) and Cancer Slope Factors (USEPA, 2005). Other uses of BMDs include comparing relative potencies (e.g., across chemicals) or relative sensitivities (e.g., across different subpopulations). Note that BMD modeling is also applicable to other fields, such as ecological risk assessment; however, this document focuses on the dose-response modeling of human health effects.
BMDs and BMDLs vs. NOAELs and LOAELs
The BMD approach was developed as an alternative to the use of No Observed Adverse Effect Level![]() No Observed Adverse Effect LevelAn exposure level at which there are no statistically or biologically significant increases in the frequency or severity of adverse effects between the exposed population and its appropriate control; some effects may be produced at this level, but they are not considered as adverse or precursors to adverse effects. In an experiment with several NOAELs, the regulatory focus is primarily on the highest one, leading to the common usage of the term NOAEL as the highest exposure without adverse effect. See also: LOAEL. (NOAEL) and Lowest Observed Adverse Effect Level
No Observed Adverse Effect LevelAn exposure level at which there are no statistically or biologically significant increases in the frequency or severity of adverse effects between the exposed population and its appropriate control; some effects may be produced at this level, but they are not considered as adverse or precursors to adverse effects. In an experiment with several NOAELs, the regulatory focus is primarily on the highest one, leading to the common usage of the term NOAEL as the highest exposure without adverse effect. See also: LOAEL. (NOAEL) and Lowest Observed Adverse Effect Level![]() Lowest Observed Adverse Effect LevelThe lowest dose or exposure level of a chemical in a study at which there is a statistically or biologically significant increase in the frequency or severity of an adverse effect in the exposed population as compared with an appropriate, unexposed control group. See also: NOAEL. (LOAEL). NOAELs and LOAELs have been used as PODs for many years in dose-response assessment but have well established limitations (see the discussion in the Benchmark Dose Technical Guidance, Section 1.2). Due to these limitations, the BMD approach is the USEPA’s preferred approach for the derivation of PODs. However, there will continue to be a need for the NOAEL/LOAEL approach because not all data sets are amenable to BMD modeling (e.g., those resulting from incomplete data availability or from a lack of models that can describe a data set adequately).
Lowest Observed Adverse Effect LevelThe lowest dose or exposure level of a chemical in a study at which there is a statistically or biologically significant increase in the frequency or severity of an adverse effect in the exposed population as compared with an appropriate, unexposed control group. See also: NOAEL. (LOAEL). NOAELs and LOAELs have been used as PODs for many years in dose-response assessment but have well established limitations (see the discussion in the Benchmark Dose Technical Guidance, Section 1.2). Due to these limitations, the BMD approach is the USEPA’s preferred approach for the derivation of PODs. However, there will continue to be a need for the NOAEL/LOAEL approach because not all data sets are amenable to BMD modeling (e.g., those resulting from incomplete data availability or from a lack of models that can describe a data set adequately).
Biological vs. Empirical Modeling
The preference in selecting suitable models for dose-response modeling is to use those that are consistent with the biological processes relevant in a particular case. Such models can include explicit expression of biological processes (e.g., cell growth dynamics, saturable enzyme processes) or covariate![]() covariateAn independent variable other than dose that may influence the outcome of an effect, e.g., age, body weight, or polymorphism. of the responses under consideration (e.g., time of response). In the absence of a biologically-based model, dose-response modeling is largely a curve-fitting exercise. The technical guidance concerns the application of these simpler dose-response models that have limited biological basis.
covariateAn independent variable other than dose that may influence the outcome of an effect, e.g., age, body weight, or polymorphism. of the responses under consideration (e.g., time of response). In the absence of a biologically-based model, dose-response modeling is largely a curve-fitting exercise. The technical guidance concerns the application of these simpler dose-response models that have limited biological basis.
Before Starting a BMD Analysis: Determining Appropriate Studies, Endpoints, and Dose-Response Data on Which to Base BMD Calculations
Preliminary steps prior to BMD modeling are discussed in Section 2.1 of the technical guidance. The steps include evaluating the toxicity database for a chemical, selecting studies to be modeled, selecting endpoints to be modeled, selecting an appropriate dose metric, and determining whether the data are sufficient for conducting a BMD analysis.
- Most datasets that show a graded monotonic response with dose will be more useful for BMD analysis.
- The minimum dataset for calculating a BMD should show a biologically or statistically significant dose-related trend in the selected endpoint(s). Having studies with one or more doses near the level of the BMR is desirable in order to give a better estimate of the BMD.
- Datasets in which all the dose levels show statistically or biologically significant changes compared with control values (i.e., there is no NOAEL) are generally useable in BMD analyses.
Section 2.1.5 of the technical guidance reviews in more detail the data evaluation steps for determining a minimum dataset necessary for calculating a BMD and includes a flowchart (Figure 2A on page 16) summarizing the evaluation criteria.
The following sections summarize some of the important issues related to study design and data reporting when using the BMD approach. The technical guidance discusses in more detail the types of data and study designs most amenable to dose-response modeling, and it allows for the possibility that NOAELs/LOAELs will continue to be used for some datasets. Resorting to the NOAEL/LOAEL approach does not resolve a data set’s inherent limitations, but it conveys that there are limitations with the data set.
Study Design
- In general, studies with more dose groups and a graded monotonic response with dose will be more useful for BMD analysis.
- Studies with only a single dose showing a response different from controls may not support BMD analysis, though if the one elevated response is near the BMR
 BMRThe response, generally expressed as in excess of background (see for example, Extra Risk), at which a benchmark dose or concentration is desired (see Benchmark Dose, Benchmark Concentration)., adequate BMD and BMDL computation may result (Kavlock et al. 1996).
BMRThe response, generally expressed as in excess of background (see for example, Extra Risk), at which a benchmark dose or concentration is desired (see Benchmark Dose, Benchmark Concentration)., adequate BMD and BMDL computation may result (Kavlock et al. 1996). - Studies in which responses are only at the same level as background or at or near the maximal response level are not considered adequate for BMD analysis. (See Section 2.1.5 of the technical guidance for more discussion.)
- It is preferable to have studies with one or more doses near the level of the BMR to give a better estimate of the BMD.
Aspects of Data Reporting
In many cases, the risk assessor must rely on summary reports of key toxicological studies, which can vary in completeness compared to the particular data requirements of the BMD method. When selecting the studies and endpoints on which to base BMD calculations and when considering the minimum dataset requirements, it's important to determine whether the summary data provides enough information for the BMD method to be applied. There are three types of endpoint data: dichotomous, continuous, and categorical.
- Dichotomous (or quantal) – A dichotomous response may be reported as either the presence or absence of an effect. Dichotomous (or quantal) data are normally reported at the individual level (e.g., 11/50 animals showed the effect). Occasionally, a dichotomous endpoint will be reported as being observed in a group with no mention of the number of animals showing the effect. This usually occurs when the incidence of the endpoint reported is ancillary to the focus of the report. For BMD modeling of dichotomous data, both the number showing the response and the total number of subjects in the group are necessary.
A special case of dichotomous data is nested dichotomous data, most often encountered in developmental toxicology studies. In the case of nested dichotomous data, pregnant animals are exposed to and effects are measured in their offspring. Nested dichotomous data can be reported in many manners: 1) total number of affected fetuses/dose, 2) number of litters with at least one fetus affected, or 3) the mean number of affected fetuses/litter (with accompanying measurement of variability). It is important to model nested dichotomous data with an appropriate model that can account for intralitter correlation (i.e., the likelihood that fetuses within a litter are more likely to respond similarly to one another than to fetuses in another litter). - Continuous – A continuous response may be reported as a measurement of the effect, such as body weights or enzyme activity, in control and exposed groups. The response might be reported in several different ways, e.g., as an actual measurement or as a contrast—relative change from control. To model continuous data when individual animal data are not available, the number of subjects, mean of the response variable, and a measure of variability (e.g., standard deviation (SD); standard error (SE); or variance) are needed for each group. The lack of a numerically reported SD or SE may preclude the calculation of a BMD. In some cases, a measure of variability is presented for the control group only and this information might be used for modeling by making an assumption, for example, that the variance in the exposed groups is the same as in the controls. However, this assumption may not be correct, and the modeling of the data and calculation of the confidence limits will not be as reliable or precise as when the variance information is available for individual groups.
- Categorical – For categorical data, more than one defined category exists in addition to the no-effect category (responses within categories are quantal). When observations in the treatment groups are characterized in terms of the severity of effect (e.g., mild, moderate, or severe histological change), these are ordered categorical data (also called ordinal data). Results may be classified by reporting an entire treatment group in terms of category (group level reporting) or by reporting the number of animals from each group in each category (individual level reporting). For example, a report of epithelial degenerative lesions might state that an exposed group showed a mild effect (group level) or that in the exposed group there were seven animals with a mild effect and three with no effect (individual level reporting). In the latter case, the BMD can be calculated using a quantal model after combining data in severity categories (e.g., model all animals with greater than a mild effect).
Dichotomous data can be viewed as a special case in which there is one effect category and the possible response is binary (e.g., effect or no effect). Modeling approaches have been discussed for categorical data with multiple categories (Dourson et al. 1985; Hertzberg 1989; Hertzberg and Miller 1985) and for group level categorical data (Guth et al. 1997; Simpson et al. 1996a, b). These models can also be used to derive a BMD by estimating the probability of effects of different levels of severity.
In addition, as for data evaluation in general, data (responses and doses) should be validated to the extent possible. For example, the original source should be examined, if possible, and any deliberate omissions of dose groups or subjects by the authors should be recognized and their basis understood. The suitability of control conditions will need to be assessed; if two types of control groups are available for the analysis, the most appropriate one is generally selected (e.g., the vehicle control).
Selecting Studies to be Modeled
Following a complete review of the toxicity data, the risk assessor selects the studies for BMD analysis, based on the human exposure situation being addressed, the quality of the studies, the reporting adequacy, and the relevance of the endpoints.
The process of selecting studies for BMD analysis is intended to identify those studies for which modeling is feasible, so that BMDs can be calculated.
All relevant studies should be considered for modeling. In some cases, the selection process will identify a single study or very few studies for which calculations are appropriate. In other cases, there may be a number of studies, or studies with a number of endpoints reported, which may require a large number of BMD calculations. In these latter cases, it may be possible to select a subset of endpoints as representative of the effects in a target organ or study. This selection can be made on the basis of sensitivity or severity, which may be more easily compared within a single study in the same target organ than across studies.
Sometimes combining several datasets may be an option (see Section 2.1.6 of the technical guidance for more discussion).
Selecting Endpoints to be Modeled
After studies have been evaluated with regard to their feasibility for BMD modeling, the selection of endpoints to model should focus on the dose-response relationships.
Typically, all endpoints within a study that the risk assessor has judged to be relevant to the exposure should be considered for modeling. This will help ensure that no endpoints with the potential of having the most sensitive effect for risk assessment applications, usually having the lowest BMDL, are excluded from the analysis.
The apparent relative sensitivities of endpoints based on NOAELs/LOAELs may not correspond to the same relative sensitivities based on BMDs or BMDLs after BMD modeling; therefore, relative sensitivities of endpoints cannot necessarily be judged a priori. For example, differences in slope (at the BMR) among endpoints could affect the relative values of the BMDLs.
Selected endpoints from different studies that have the potential to be used in the determination of a POD(s) should all be modeled, especially if different UFs may be used for different studies and endpoints. The risk assessor selects the BMDL(s) to serve as the POD(s) using scientific judgment and principles of risk assessment as well as the results of the modeling process.
Note that it is sometimes desirable to carry through risk estimate derivations for multiple endpoints for comparisons and other purposes.
Minimum Dataset for Calculating a BMD
- There should be at least a statistically or biologically significant dose-related trend in the selected endpoint.
- The dataset should contain information on the dose-response relationship between the extremes of the control level and the maximal response observed. An ideal situation is to have one or more data points near the BMR.
- Refer to section 2.1.5 of the technical guidance for examples that illustrate failure to meet these criteria.
Combining Data for a BMD Calculation
Datasets that are statistically and biologically compatible may be combined prior to dose-response modeling, resulting in increased confidence, both statistical and biological, in the calculated BMD.
The simplest approach to combining datasets is to treat the data as if they were all collected simultaneously. If it is plausible that the multiple datasets represent a homogeneous picture of the dose-response (for example, the responses at doses common to two or more datasets are essentially the same and statistically undifferentiable), then this is a justifiable approach.
It is likely there will be some variability among datasets, requiring more elaborate modeling to combine information properly. There is as yet too little practical, as well as theoretical, experience with this situation to provide specific guidance in the matter, other than to say that statistically appropriate methods and biological judgment must be used and justified if datasets are combined for modeling.
Dosimetric Adjustments
Often dosimetric adjustments are used to convert the doses administered to experimental animals into lifetime continuous human-equivalent doses (HEDs, e.g., USEPA 1994, 2002a, 2011). While it is beyond the scope of this material to provide guidance for deriving or applying these adjustments, this section notes some general circumstances in which dosimetric adjustments may be important to consider prior to dose-response modeling.
It is generally preferable to model the experimental animal response data with experimental animal doses (e.g., applied dose, internal dose metric), in order to describe the dose-response relationship before any assumptions about interspecies extrapolation are invoked.
- If the adjustment is proportional across the doses (e.g., a constant, linear adjustment for continuous exposure), then whether one adjusts the doses before or after the modeling does not affect the end results and is more a matter of convenience.
- If, however, the adjustments are not proportional across the doses, then it may be more suitable to make the dosimetric adjustments before the dose-response modeling. This could be the case, for example, when the available data only support interspecies scaling through body weight scaled to the ¾-power and the body weights differ notably across dose groups.
Similarly, physiologically based pharmacokinetic (PBPK) modeling often reflects processes that are nonlinear with dose. When PBPK model-derived dose metrics are available, multiple options may merit consideration.
- The relationship between external concentrations and internal dose metrics must be considered carefully when using PBPK modeling in conjunction with the BMD approach.
- If the relationship between external/internal dose metrics is linear across doses, curve fitting using the experimental exposure doses/concentrations can be used to estimate the BMD/BMDL, which can then be converted to the human equivalent values or to the levels of a pertinent dose metric (e.g., area under the curve of metabolite concentration in the liver) using an experimental animal PBPK model.
- However, if the relationship is not linear, conversion of external concentrations into internal doses must be done prior to BMD modeling to account for the underlying non-linear toxicokinetic and metabolic processes.
- For highly supralinear dose-response relationships there may be difficulties adequately fitting a curve using applied doses, so it may be advantageous to use an internal dose metric for the dose-response modeling.
- If an internal dose metric from an experimental animal PBPK model is used, the HEDs for the BMD and BMDL would be back-calculated through a human PBPK model or estimated in some other way.
- Dose-response analyses in terms of an internal dose metric may simplify the dose-response relationship (e.g., linearize a supralinear curve due to metabolic saturation), potentially improving curve fitting, and may help elucidate the contributions of the pharmacokinetic processes versus the pharmacodynamic processes to the observed dose-response relationship.
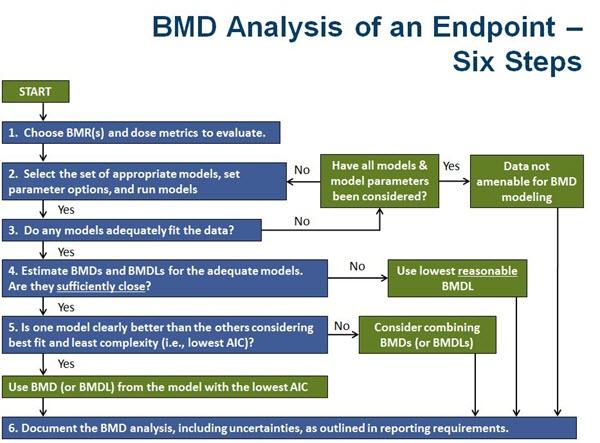
Decision Tree for BMD Modeling
After you have determined the studies, endpoints and dose metrics that are appropriate for BMD modeling, you can begin the analysis process.
The decision tree below summarizes the general progression of steps in a BMD/BMDL calculation for each candidate endpoint/study combination. A separate BMD calculation supports each endpoint/study combination that is a reasonable candidate for a final quantitative risk estimate. Unlike comparing NOAELs or LOAELs across endpoints or studies, the relative values of potential BMDs are not readily transparent until after the modeling has been completed.
The decision tree steps and its supporting methods are discussed in more detail on the rest of this page.
- Select the BMR based on the type of data (i.e., quantal versus continuous), sensitivity of study design, toxicity endpoint, and judgments about the adversity of the specified level of change in the endpoint if continuous. See Selecting the Benchmark Response Level (BMR) on this page.
- Model the dose-response data, using model structures specific to the type of data (i.e., quantal versus continuous, depending on how the BMR is defined) and study design (e.g., nested). For modeling cancer bioassay data, a specific default algorithm is generally used except for case-specific situations in which an alternate model may be superior (e.g., a time-to-tumor model or a biologically-based model). For other types of experimental animal data, curve-fitting can be attempted with a variety of models. Human data are modeled in a case-specific way and may need to account for covariates, such as competing causes of mortality. See Selecting the Model on this page.
- Assess the fit of the models. Retain models that are not rejected using a p-value of 0.1 (except when there is an a priori model preference; see Section 2.3.5 of the technical guidance). Examine the residuals and plot the data and models; check that the models adequately describe the data, especially in the region of the BMR. Sometimes it may be necessary to transform the data in some way or to conduct further statistical evaluations in order to get a good fit. See Assessing How Well the Model Describes the Data on this page.
- Calculate 95% lower confidence limits on the candidate BMDs (i.e., BMDLs) using the models that adequately fit the data. See Calculating Confidence Limits to Get a BMDL on this page.
- Select from among the models that adequately fit the data. If the BMDL values from these remaining models are sufficiently close (given the needs of the assessment), the model with the lowest AIC may be selected to provide the BMDL. If the BMDL values are not sufficiently close, some model dependence is assumed, and a science policy judgment may need to be made. See Comparing Models on this page.
- Document the BMD analysis as outlined in the Reporting Recommendations on this page.
Selecting the Benchmark Response Level (BMR)
The following describes options used for selecting the BMR based on the type of data (quantal vs. continuous). This is only one criterion, however. One should also consider sensitivity of study design, toxicity endpoint, and judgments about the adversity of the specified level of change in the endpoint if continuous.
For quantal (dichotomous) data, the conventional approaches are fairly straightforward. Refer to the "Dichotomous Model Descriptions" and "Dichotomous Model Options Fields" sections of the BMDS User Manual for more information.
For continuous data, on the other hand, there is less historical precedence upon which to draw; however, some reasonable options are presented. The rationale supporting each selected BMR should be provided. Once a BMR is selected and the dose-response data are modeled, the BMD is explicitly determined. Refer to the "Continuous Model Descriptions" and "Continuous Model Options Fields" sections of the BMDS User Manual for more information.
For Quantal Data
- An extra risk of 10% is recommended as a standard reporting level for quantal data, for the purposes of making comparisons across chemicals or endpoints. The 10% response level has customarily been used for comparisons because it is at or near the limit of sensitivity in most cancer bioassays and in noncancer bioassays of comparable size. Note that this level is not a default BMR for developing PODs or for other purposes.
- Biological considerations may warrant the use of a BMR of 5% or lower for some types of effects (e.g., frank effects), or a BMR greater than 10% (e.g., for early precursor effects) as the basis of a POD for a reference value.
- Sometimes, a BMR lower than 10% (based on biological considerations), falls within the observable range. From a statistical standpoint, most reproductive and developmental studies with nested study designs easily support a BMR of 5%. Similarly, a BMR of 1% has typically been used for quantal human data from epidemiology studies. In other cases, if one models below the observable range, one needs to be mindful that the degree of uncertainty in the estimates increases. In such cases, the BMD and BMDL can be compared for excessive divergence. In addition, model uncertainty increases below the range of data.
For Continuous Data
- Preferred approach: If there is a minimal level of change in the endpoint that is generally considered to be biologically significant, then that amount of change can be used to define the BMR.
- If individual data are available and a decision can be made about which individual levels can be reasonably considered adverse, then the data can be implicitly dichotomized using the hybrid model or explicitly dichotomized based on that cutoff value, and the BMR can be set as above for quantal data. Note that implicit dichotomization is preferred over explicit dichotomization, because of the loss of information associated with the latter.
- In the absence of any other idea of what level of response to consider adverse, a change in the mean equal to one control SD (or lower, e.g., 0.5 SD, for more severe effects) from the control mean should be used.
For more details on this step, see Section 2.2 of the technical guidance.
Modeling the Data
The goal of the mathematical modeling in BMD computation is to fit a model to dose-response data that describes the dataset, especially at the lower end of the observable dose-response range. The fitting must be done in a way that allows the uncertainty associated with parameter estimates to be quantified and related to the estimate of the dose that would yield the BMR. In practice, this procedure will involve first selecting a family or families of models for further consideration, based on characteristics of the data and experimental design, and fitting the models using one of a few established methods. Subsequently, BMDs and BMDLs are calculated at the BMR(s).
The preference in selecting suitable models is to use those that are consistent with the biological processes understood to operate in a particular case and to avoid models that are clearly inconsistent. In the absence of a biologically based model, dose-response modeling is largely a curve-fitting exercise among the variety of available empirical models. Currently there is no recommended hierarchy of models that would expedite model selection, in part because of the many different types of datasets and study designs affecting dose-response patterns. As more flexible models are developed, hierarchies for some categories of endpoints will likely be more feasible. Refer to the "Model Descriptions" section of the BMDS User Manual for more information.
Selecting the Model
- The nature of the measurement that represents the endpoint of interest and the experimental design used to generate the data.
- Certain constraints on the models or their parameter values sometimes need to be observed and may influence model selection.
- Desirability of modeling multiple endpoints at the same time.
The diversity of possible endpoints and shapes of their dose-response relationships for different agents precludes specifying a small set of models to use for BMD computation. This will inevitably lead to the need for judgment when selecting the final model and BMD/BMDL for dose-response assessment. As experience using BMD methodology in dose-response assessment accumulates, it may be possible to narrow the number of models to a few that are sufficiently flexible and non-redundant to be specified for certain scenarios.
Type of Endpoint
- Dichotomous variables. Data on dichotomous variables are commonly presented as a fraction or percent of individuals that exhibit the given condition at a given dose or exposure level. Note that for modeling dichotomous data, one uses the exact counts. For such endpoints, normally we select probability density models like logistic, probit, Weibull, and so forth, whose predictions lie between zero and one for any possible dose, including zero.
- Continuous variables. Data for continuous variables are often presented as means and SDs or SEs but may also be presented as a percent of control or some other standard. From a modeling standpoint, the most desirable form for such data is by individual. Unlike the usual situation for dichotomous variables, summarization of continuous variables results in a loss of information about the distribution of those variables. In addition, individual data is required when the intention is to use covariates in the analysis.
- If the BMR is defined as a level of change in a continuous endpoint (usually expressed as a particular change in the mean response, possibly as a fraction of the control mean, or as a fraction of the SD of the measurement from untreated individuals), a continuous model can be used. Typical continuous models include polynomial models, power models, and Hill models.
- If the data are dichotomized and the BMR is defined as the proportion of individuals with more than a specified level of change in the continuous endpoint, the resulting variable can be modeled as dichotomous. Recall, however, that dichotomization results in a loss of information and should generally be avoided.
An alternative is to use a hybrid approach, such as that described by Gaylor and Slikker (1990), Kodell et al. (1995), and Crump (1995), which fits continuous models to continuous data, and, presuming a distribution of the data, calculates a BMD in terms of the fraction affected. Using this approach, the probability (risk) of an individual with an adverse level can be estimated directly as a function of dose. For more information, see Section 2.3.3.1 of the technical guidance.
Experimental Design
The aspects of experimental design that bear on model selection include the total number of dose groups used and possible clustering of experimental subjects.
The number of dose groups has a bearing on the number of parameters that can be estimated—the number of parameters that affect the overall shape of the dose-response curve normally cannot exceed the number of dose groups.
Clustering of experimental subjects is actually more of an issue for methods of fitting the models than for choice of the model form itself. The most common situation in which clustering occurs is in developmental toxicity experiments, where the agent is administered to the mothers and individual offspring within litters are examined for adverse effects. For more information, see Appendix A, Example A.5 in the technical guidance.
Another example of clustering concerns designs in which individuals yield multiple observations (repeated measures). This can happen, for example, when each subject receives both treatment and control (common in studies with human subjects), or when each subject is observed multiple times after treatment (e.g., neurotoxicity studies). The issue in all these examples is that individual observations cannot be taken as independent of each other. Most methods used for fitting models rely heavily on the assumption that the data are independent, and special fitting methods need to be used for datasets that exhibit more complicated patterns of dependence. (See for example, Ryan 1992a, b; Davidian and Giltinan 1995.)
Constraints
In dose-response modeling, the modeler may need to consider choices that constrain the set of parameter values that are numerically possible—typically for the purpose of strengthening the biological plausibility of the results. For more information on the constraint options available in BMDS models, refer to the "Model Options Screens" sections of the BMDS User Manual for more information. Note that available constraint options vary among models.
An obvious constraint on models for dichotomous data is that probabilities are restricted to being positive numbers no greater than one. Biological realities impose other clear constraints on models. For example, most biological measures are positive; therefore, models should be selected so that their predicted values, at least in the region of application, conform to that constraint.
Other choices have to do with the biological plausibility of dose-response patterns. For many toxic effects, a monotonic increase in effect with dose will be expected—that is, a higher dose will have an equal or greater effect than a lower dose. Thus, much existing practice has constrained models to be monotonic, for example in the fitting of the multistage model, the parameters are constrained to be nonnegative. In some circumstances non-monotonic relationships may be seen, most commonly when there are qualitatively altered biological mechanisms or observational limitations with high-dose data (see Section 2.3.6 of the technical guidance.)
Other questions arise with models that can be steeply supralinear for some parameter values. In models in which dose is raised to a power that is a parameter to be estimated (such as a Weibull model), the slope of the dose-response curve becomes very steep at low doses for power parameter values less than 1. This can raise difficult questions for the assessor. On the one hand, it is not uncommon for data in the observed range to show a supralinear response pattern (e.g., shape of Michaelis-Menten relationship), so excluding power parameters less than 1 may not provide the best fit to the data or allow adequate evaluation of uncertainty in response in the observed range. In principle, as BMD modeling does not generally seek to extrapolate to very low doses, the high slopes seen for some unconstrained models near the origin is not in itself a fundamental problem. On the other hand, in some instances, calculated BMDs and BMDLs can be very low when the power parameter is less than 1. This reflects the fact that the data do not constrain the lower end of the dose-response curve.
In general, the modeler should consider constraining power parameters to be 1 or greater (this is the default in the BMDS application for most models) For details on BMDS default settings that restrict specific parameters, refer to the BMDS User Manual's "Appendix B: Model Options Screen Fields Reference."
However, if the observed data do appear supralinear, unconstrained models or models that contain an asymptote term (e.g., a Hill model) warrant investigation to see whether they can support reasonable BMD and BMDL values. If they cannot, other model forms should be considered for a POD; at times, modeling will not yield useful results and the NOAEL/LOAEL approach might be considered, although the data gaps and inherent limitations of that approach should be acknowledged.
In quantal models, often a background parameter quantifies the probability that the outcome being modeled can occur in the absence of exposure. It may be tempting to reduce the number of parameters to be estimated by fixing the value of the background parameter to be zero. However, only when it is clear that an outcome would not occur in the absence of the exposure is it appropriate to fix the value of the background to zero (e.g., modeling mortality and acute exposures).
Inclusion of a so-called “threshold” term in the models is generally not recommended for BMD analysis. Although such a parameter is not an estimate of a biological threshold, it is easily mistaken for one due to confusing terminology. Furthermore, most datasets can be fit adequately without this parameter and the associated loss of a degree of freedom. However, on rare occasions, the increase in a response may be so precipitous that including a threshold parameter is needed for dose-response modeling with commonly available models, and in such cases including the parameter is acceptable.
Covariates
Including a covariate![]() covariateAn independent variable other than dose that may influence the outcome of an effect, e.g., age, body weight, or polymorphism. on individuals is sometimes desirable when fitting dose-response models. For example, litter size has often been included as a covariate in modeling laboratory animal data in developmental toxicity studies. For more information on how BMDS nested models implement this, refer to the "Nested Model Descriptions" section of the BMDS User Manual.
covariateAn independent variable other than dose that may influence the outcome of an effect, e.g., age, body weight, or polymorphism. on individuals is sometimes desirable when fitting dose-response models. For example, litter size has often been included as a covariate in modeling laboratory animal data in developmental toxicity studies. For more information on how BMDS nested models implement this, refer to the "Nested Model Descriptions" section of the BMDS User Manual.
Another example is in modeling epidemiology data when certain covariates (e.g., age, parity) are included that are expected to affect the outcome and might be correlated with exposure. If the covariate has an effect on the response, including it in a model may improve the precision of the overall estimate by accounting for variation that would otherwise end up in the residual variance. Any variable that is correlated (non-causally) with dose and which affects outcome should be considered as a covariate.
Model Fitting
The goal of the fitting process is to find values for all the model parameters so that the resulting fitted model describes those data as well as possible; this is termed “parameter estimation.” One way to achieve this is to identify a function (the objective function) of all the parameters and all the data with the property that the parameter values that correspond to an overall minimum (or, equivalently, an overall maximum) of the function give the desired model predictions.
- Dichotomous data—an example of such a situation is the case of individual independently treated animals (i.e., not clustered in litters) scored for the presence of a single response. Here it is reasonable to suppose that the number of responding animals follows a binomial distribution with the probability of response expressed as a function of dose.
- Continuous variables, especially means of several observations, are often normal (Gaussian) or log-normal. When variables are normally distributed with a constant variance, minimizing the sum of squares is equivalent to maximizing the likelihood, which explains in part why least squares methods are often used for continuous variables.
- In developmental toxicity data, the pregnant mother is the experimental unit and statistical methods must account for the tendency of littermates to respond similarly. The distribution of the number of animals with an adverse outcome is often taken to be approximately beta-binomial, in order to accommodate the lack of independence among littermates (litter effect; e.g., Chen and Kodell 1989; Williams 1975). One disadvantage of this method is a lack of robustness if the litter effect is modeled incorrectly (Kupper et al. 1986; Williams 1988). Alternative analyses can be based on quasi-likelihood, or more generally, generalized estimating equations. A simple approach using a simple data transformation has been described by Rao and Scott (1992) and Krewski and Zhu (1995) and has been shown to be as efficient as either the GEE or the maximum likelihood approach (Fung et al. 1998).
Refer to Section 2.3.4 of the technical guidance more details on these methods.
Assessing How Well the Model Describes the Data
Global Goodness of Fit Measures (p values)
An important criterion for selecting a fitted model is that the model provides an adequate description of the data, especially in the region of the BMR. Most fitting methods will provide a global goodness-of-fit![]() goodness-of-fitA statistic that measures the dispersion of data about a dose-response curve in 44 order to provide a test for rejection of a model due to lack of an adequate fit, e.g., a P-value < 0.1. measure, usually a p-value
goodness-of-fitA statistic that measures the dispersion of data about a dose-response curve in 44 order to provide a test for rejection of a model due to lack of an adequate fit, e.g., a P-value < 0.1. measure, usually a p-value![]() p-valueIn testing a hypothesis, the probability of a type I error (false positive). The probability that the sample (experimental) results are compatible with a specific hypothesis.. These measures quantify the degree to which the dose-group responses that are predicted by the model differ from the actual dose-group response, relative to how much variation of the dose-group response one might expect. Small p-values indicate that a value of the goodness-of-fit statistic at least this extreme is unlikely to have been achieved if the data were actually sampled from the model, and, consequently, the model is a poor fit to the data. Since BMD modeling is usually a curve-fitting exercise involving a suite of models and since it is important that the data be adequately modeled for BMD calculation, it is recommended that α = 0.1 be used to compute the critical value for goodness-of-fit, instead of the more conventional values of 0.05 or 0.01.
p-valueIn testing a hypothesis, the probability of a type I error (false positive). The probability that the sample (experimental) results are compatible with a specific hypothesis.. These measures quantify the degree to which the dose-group responses that are predicted by the model differ from the actual dose-group response, relative to how much variation of the dose-group response one might expect. Small p-values indicate that a value of the goodness-of-fit statistic at least this extreme is unlikely to have been achieved if the data were actually sampled from the model, and, consequently, the model is a poor fit to the data. Since BMD modeling is usually a curve-fitting exercise involving a suite of models and since it is important that the data be adequately modeled for BMD calculation, it is recommended that α = 0.1 be used to compute the critical value for goodness-of-fit, instead of the more conventional values of 0.05 or 0.01.
An exception to this recommendation is when there is an a priori reason to prefer a specific model(s), in which case the more conventional values of α = 0.05 or α = 0.01 may be considered. P-values cannot be compared from one model to another since they are estimated under the assumption that the different models are correct; they can only identify those models that are consistent with the experimental results. When there are other covariates in the models, such as litter size, the idea is the same, but the calculations are more complicated. In this case, the range of doses and other covariates is broken up into cells, and the number of observations that fall into each cell is compared to that predicted by the model.
For more information on p-values derived by BMDS models, refer to the "Tests of Fit" section of the BMDS User Manual.
Scaled Residuals at Each Dose Level
It can happen that the model is never very far from the data points (so the p-value for the goodness-of-fit statistic is not too small) but is always on one side or the other of the dose-group means. Also, there could be a wide range in the response, and the model could predict the high-dose responses well but miss the low-dose responses. In such cases, the goodness-of-fit statistic might not be significant, but the fit should be treated with caution. One way to detect such situations is with tables or plots of residuals, measures of the deviation of the response predicted by the model from the actual data. If the residuals are scaled by their estimated variability (SE), then such scaled, or standardized, residuals that exceed 2 in absolute value warrant further examination of the model fit.
For more information on the scaled residuals derived by BMDS models, refer to the BMDS User Manual section, "Dichotomous Model Text Output."
Graphical Displays
Another way to detect the form of these deviations from fit is with graphical displays. Plots should always supplement goodness-of-fit testing. It is extremely helpful that plots that include data points also include a measure of dispersion of those data points, such as confidence limits. Refer to the BMDS User Manual section on "Viewing Plots" for more information.
Improving Model Fit
- Whenever none of the available models provides an adequate fit to the data, the modeler should first (re)consider data quality or experimental problems that may have been missed in the initial study evaluation (e.g., opportunistic infections, dosing errors).
- Sometimes, adjustments to the data (e.g., a log-transformation of dose or adjustments for unrelated deaths) may be necessary. Some plateauing or non-monotonic response patterns may be better understood in the context of progression to, or masking by, other responses more prevalent at higher exposures, suggesting that a broader definition of the response should be considered.
- Use of a more complex model (e.g., a model accounting for time of response) may be supported by the available data. Or there may be relevant pharmacokinetic data or models (e.g., addressing saturation of metabolic systems or delivery systems for the ultimate toxic substance, or other complex pharmacokinetics) that could provide a suitable dose metric yielding a dose-response relationship more easily fit by readily available models.
- At times a lack of fit may be due to aspects of the model-fitting process, e.g., whether the nonlinear fitting procedure really arrived at the “best” estimates, or whether the impact of any heterogeneous variances has been adequately taken into account. It is always good practice when fitting models that are nonlinear in parameters to try different initial values, just in case the estimation process has converged in a less representative set of parameter estimates.
- Heterogeneous variances can adversely impact continuous model fits, including the estimate of the standard deviation used as a BMR. One approach is to model the variance as proportional to the mean raised to a power. Refer to the BMDS User Manual section on "Continuous Model Descriptions" for more information on how variance data are modeled in BMDS.
- When a lack of fit persists, one option is to look for a more flexible empirical model that can adequately describe the dose-response relationship. A seeming advantage to this approach is that one may be able to incorporate all the data into the analysis. A danger in this approach is that the attempt to fit the data in a particular portion of the dose range may skew the dose-response curve in the dose range of more direct interest. In many situations the BMD is close to the lowest doses in the study, and thus the modeler can evaluate the goodness-of-fit of the model in the area of the BMD.
For more details, including guidance on when or if to drop dose groups to improve model fit, refer to Section 2.3.6 and Appendix A example cases in the technical guidance.
Comparing Models
Often, several models provide an adequate fit to a given dataset. At this time, risk modelers are encouraged to select a well-fitting and plausible model. The following guidance is provided for use in comparing model fit.
A set of adequately fitting models may be essentially unrelated to each other (for example a logistic model and a probit model often do about as well at fitting dichotomous data) or they may be related to each other in the sense that they are members of the same family that differ in which parameters are fixed at some default value. For example, one can consider the log-logistic, the log-logistic with non-zero background, and the log-logistic with threshold and non-zero background all to be members of the same family of models. Goodness-of-fit statistics are not designed to compare different models—in particular, a higher goodness-of-fit p-value for one model does not necessarily indicate a better fit over another model with a lower p-value so alternative approaches to selecting a model to use for BMD computation need to be pursued.
Appendix A of the technical guidance provides a number of examples (Examples A.1–A.5) exploring issues in model fit and model comparison.
Within a Family of Models: the Akaike Information Criterion (AIC)
Within a family of dose-response models, as additional parameters are introduced, the fit will generally improve. Likelihood ratio tests can be used to evaluate whether the improvement in fit afforded by estimating additional parameters is justified. Such tests cannot be applied to compare statistical models from different families (i.e., lognormal versus normal). Some statistics, notably Akaike's Information Criterion (AIC, Akaike 1973; Linhart and Zucchini 1986; Stone 1998; AIC is −2L + 2p, where L is the log-likelihood at the maximum likelihood estimates [MLEs] for p estimated parameters), can be used to compare models from different families using a similar fitting method (for example, least squares or a binomial maximum likelihood). Although such methods are not exact, they can provide useful guidance in model selection.
Refer to the "Continuous Model Maximum Likelihood" section of the BMDS User Manual for more information.
Other Considerations
When other datasets for similar endpoints exist, an external consideration can be applied. It may be possible to compare the result of BMD computations across studies if all the data were fit using the same form of model, presuming that a model can be found that describes all the datasets. Another consideration is the existence of a conventional approach to fitting a particular kind of data. Neither of these considerations should be seen as justification for using ill-fitting models. Finally, it is often considered preferable to use models with fewer parameters, when possible.
Calculating Confidence Limits to Get a BMDL
A confidence interval![]() confidence intervalAn interval defined by two values, called confidence limits, calculated from sample data using a procedure which ensures that the unknown true value of the quantity of interest falls between such calculated values in a specified percentage of samples. Commonly, the specified percentage is 95%; the resulting confidence interval is then called a 95% confidence interval. A one-sided confidence interval is defined by a single calculated value called an upper (or lower) confidence limit. "The numerical interval constructed around a point estimate of a population parameter, combined with a probability statement (the confidence coefficient) linking it to the population's true parameter value. If the same confidence interval construction technique and assumptions are used to calculate future intervals, they will include the unknown population parameter with the same specified probability" (QAMS 1993, 6). expresses the uncertainty in a parameter estimate that is due to sampling and/or measurement error. Quantifying “confidence” comes from carrying out the conceptual experiment of infinitely replicating the experiment that generated the data being analyzed. The “confidence” or “coverage” associated with the confidence interval is the fraction of these repeated intervals that include the parameter being estimated, for example, the BMD.
confidence intervalAn interval defined by two values, called confidence limits, calculated from sample data using a procedure which ensures that the unknown true value of the quantity of interest falls between such calculated values in a specified percentage of samples. Commonly, the specified percentage is 95%; the resulting confidence interval is then called a 95% confidence interval. A one-sided confidence interval is defined by a single calculated value called an upper (or lower) confidence limit. "The numerical interval constructed around a point estimate of a population parameter, combined with a probability statement (the confidence coefficient) linking it to the population's true parameter value. If the same confidence interval construction technique and assumptions are used to calculate future intervals, they will include the unknown population parameter with the same specified probability" (QAMS 1993, 6). expresses the uncertainty in a parameter estimate that is due to sampling and/or measurement error. Quantifying “confidence” comes from carrying out the conceptual experiment of infinitely replicating the experiment that generated the data being analyzed. The “confidence” or “coverage” associated with the confidence interval is the fraction of these repeated intervals that include the parameter being estimated, for example, the BMD.
The consequences of this conceptual experiment are generally converted into an algorithm for computing the confidence limits![]() confidence limitsTwo statistics that form the upper and lower bounds of a confidence interval., and statistical theory is used to calculate intervals with a given level of coverage. The choice of confidence level represents tradeoffs in data collection costs and the needed data precision. Just as 0.05 is a conventional cut-off level for significance tests (though not necessarily preferred for all data), 95% is a convenient choice for most limits and is the default value recommended in this guidance. The ends of a confidence interval are called confidence limits. Confidence limits bracket those values which, within a particular model family, are consistent with the data, but they do not account for or assume any correspondence between the modeled animal data and the human population of concern. With rare but important exceptions, calculated CIs are approximations, in the sense that the actual coverage of the interval usually diverges somewhat from the desired level.
confidence limitsTwo statistics that form the upper and lower bounds of a confidence interval., and statistical theory is used to calculate intervals with a given level of coverage. The choice of confidence level represents tradeoffs in data collection costs and the needed data precision. Just as 0.05 is a conventional cut-off level for significance tests (though not necessarily preferred for all data), 95% is a convenient choice for most limits and is the default value recommended in this guidance. The ends of a confidence interval are called confidence limits. Confidence limits bracket those values which, within a particular model family, are consistent with the data, but they do not account for or assume any correspondence between the modeled animal data and the human population of concern. With rare but important exceptions, calculated CIs are approximations, in the sense that the actual coverage of the interval usually diverges somewhat from the desired level.
Confidence intervals (CIs) can be two-sided, bounding their corresponding parameter values on both sides, or one-sided, bounding their corresponding parameter values on only one side. So, for example, a one-sided interval is used to help ensure that the true value of the BMD is not less than a specified value.
A lower confidence limit is placed on the BMD to obtain a dose (BMDL) that assures with high confidence (e.g., 95%) that the BMR is not exceeded. This process rewards better experimental design and procedures that provide more precise estimates of the BMD, resulting in tighter CIs and thus higher BMDLs.
A detailed discussion of how BMDLs are calculated is beyond the scope of this page. Some procedures and examples for calculating BMDLs are given by Gaylor et al. (1998) and are discussed in the technical guidance. Refer to Section 2.3.8 of the technical guidance for more details on methods to calculate the confidence limit(s) at the selected BMR using the model and the same estimation procedure as for the BMD. For information on how BMDS models estimate BMDLs, refer to the BMDS User Manual section, "Quantal Models with Background Dose Parameter."
Selecting the Model to Use for POD Computation
The following approach is recommended for selecting the model(s) to use for computing the BMDL to serve as the POD for a specific dataset (for a graphical illustration of these concepts see the six-step procedure pictured above in Decision Tree for BMD Modeling). As noted earlier, some of these decisions are best performed by or in collaboration with personnel expert in the statistical procedures and potential pitfalls of this type of analysis.
- Assess goodness-of-fit, using a value of α = 0.1 to determine a critical value (or α = 0.05 or α = 0.01 if there is reason to use a specific model(s) rather than fitting a suite of models; see Section 2.3.5 of the technical guidance).
- Further reject models that apparently do not adequately describe the relevant low-dose portion of the dose-response relationship, examining residuals and graphs of models and data. (See Section 2.3.5 of the technical guidance)
- As the remaining models have met the recommended default statistical criteria for adequacy and visually fit the data, any of them theoretically could be used for determining the BMDL. The remaining criteria for selecting the BMDL are necessarily somewhat arbitrary and are suggested as defaults.
- If the BMDL estimates from the remaining models are sufficiently close (given the needs of the assessment), reflecting no particular influence of the individual models, then the model with the lowest AIC may be used to calculate the BMDL for the POD. This criterion is intended to help arrive at a single BMDL value in an objective, reproducible manner. If two or more models share the lowest AIC, the simple average or geometric mean of the BMDLs with the lowest AIC may be used. Note that this is not the same as “model averaging”, which involves weighing a fuller set of adequately fitting models. (See Section 2.3.7 of the technical guidance.) In addition, such an average has drawbacks, including the fact that it is not a 95% lower bound (on the average BMD); it is just the average of the particular BMDLs under consideration (i.e., the average loses the statistical properties of the individual estimates).
- If the BMDL estimates from the remaining models are not sufficiently close, some model dependence of the estimate can be assumed. Expert statistical judgment may help at this point to judge whether model uncertainty is too great to rely on some or all of the results. If the range of results is judged to be reasonable, there is no clear remaining biological or statistical basis on which to choose among them, and the lowest BMDL may be selected as a reasonable conservative estimate. Additional analysis and discussion might include consideration of additional models, the examination of the parameter values for the models used, or an evaluation of the BMDs to determine if the same pattern exists as for the BMDLs. Discussion of the decision procedure should always be provided.
- In some cases, modeling attempts may not yield useful results. When this occurs and the most biologically relevant effect is from a study considered adequate but not amenable to modeling, the NOAEL (or LOAEL) could be used as the POD. The modeling issues that arose should be discussed in the assessment, along with the impacts of any related data limitations on the results from the alternate NOAEL/LOAEL approach.
Reporting Requirements
EPA requires thorough justification of the decisions made to support the chosen approach and values. The BMDS Wizard report generation feature was designed to facilitate the proper reporting of essential elements of a dose-response for risk assessment purposes.
- Study or studies selected for BMD calculation(s)
- Rationale for study selection
- Rationale for selection of endpoints (effects)
- A list of the dose-response data used
- Dose-response model(s) chosen for each case
- Rationale
- Estimation procedure (e.g., maximum likelihood, least squares, generalized estimating equations)
- Estimates of model parameters
- Goodness-of fit (e.g., chi-squared statistics), log-likelihood, and AIC
- Standardized residuals (observed minus predicted response/SE)
- Choice of BMR for each case
- Rationale
- Procedure used if for continuous data
- Computation of the BMD for each case
- Calculation of the lower confidence limit for the BMD (i.e., the BMDL) for each case
- Confidence limit procedure (e.g., likelihood profile, delta method, bootstrap)
- BMDL value
- Graphics for each case
- Plot of fitted dose-response curve with data points and error (SD) bars
- Plot of confidence limits for the fitted curve (optional; if included, the narrative describes the methods used to compute them)
- Identification of the BMD and BMDL
- BMDs and BMDLs for standardized BMRs (for comparisons)
- For dichotomous data, the BMD and BMDL for an extra risk of 0.10
- For continuous data, the BMD and BMDL corresponding to a change in the mean response equal to 1 control SD from the control mean.
- BMDU (upper confidence limit for the BMD), depending on the application and feasibility of estimation